love dem logs



Logging Logs
Logs show up everywhere in ML. Most of my graduate degree was an exercise in remembering to take the log of both sides, so that I could turn a compound multiplication into a linear sum
In finance, we also primarily focus on taking log-returns. I will go into some detail as to why this is preferable
Log Odds
When fitting a binary logistic regression model, you will recall that the objective function is a log odds, that is, log(p / (1-p)). Why do we do this? Odds are sort of an intuitive objective function, you want to maximize the ratio of "getting it right". But the log part is a bit confusing. We use log odds because the support of log(x) is (-inf, +inf). When we look at just odds: p / (1-p), we are bounded (0, +inf). Having the entire real number line as support is useful when trying to fit functions, as it makes the gradient update step much easier, and we do not have to add additional constraints on the function we are approximating. (of-course you could clip, but that intuitively feels like a sub optimal soln).
Log Returns
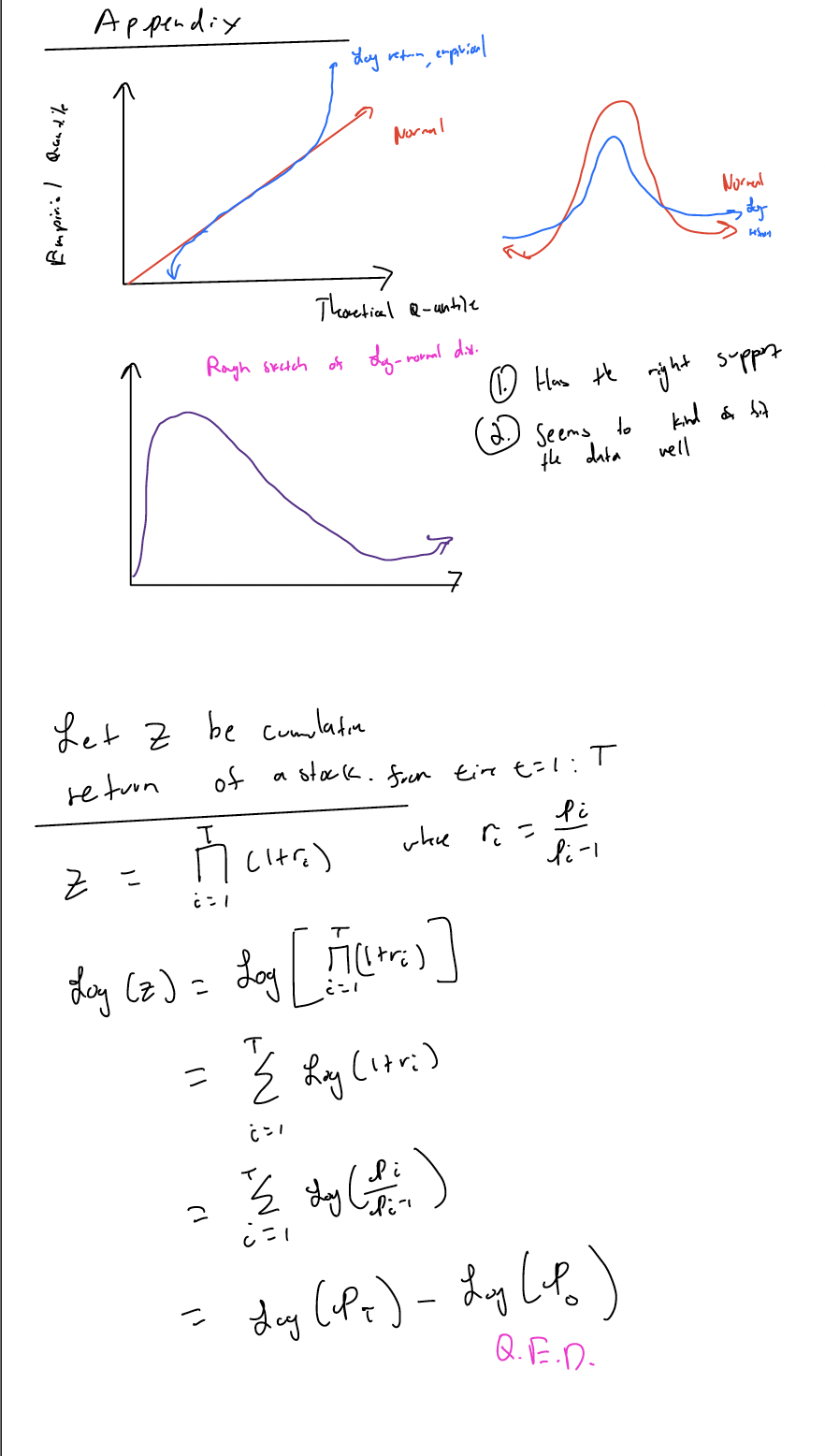
What's so special about log-returns? For one, we have a similar sort of issue as with log odds. a return is defined as p_i / (p_i_1), where p_{i} is the price at time i of a financial security. Thus, one finds a similar argument for the "support". We also can make the claim that log "squishes" highly positive returns (as evidenced by looking at the function), so as to make returns overall more symmetric. If one looks at the appendix below, we have plotted a QQ plot comparing log-returns of a sample stock with that of a normal distribution. We see that it has the same symmetry as the normal distribution, but also has a bit more of fat tails at the end( shown on the right).
We can also make the argument that prices actually follow a log-normal distribution (shown in the appendix). If prices follow a log-normal distribution, then log(returns) is log(price/ price) which is log(price) - log(price), which turns into the subtraction of two normally distributed variables, which itself must be a normal distribution. Thus, we have theoretical properties/justifications that may be useful for us to think through when dealing with more data.
Finally, perhaps the most important aspect of using log returns is the fact that if I look at two time points, I can run log(p_t) - log(p_t_2) to get the cumulative log return. If I was dealing with just return, this would not be possible, as I would have to run the multiplication operation over the entire sequence. The proof, shown in the appendix, utilizes the properties of logs to estimate the cumulative log return in a simple step. This can then, of course, be easily converted to the actual return by taking an exponential.